Some Exercises on the Mathematics of the DFT
This file develops some basic theory of the DFT formally using the Coq Theorem Prover. We follow a standard reference, whose proofs are quoted here for reference: https://ccrma.stanford.edu/~jos/mdft/
We will first define circular signals, and associated operations like shifting and convolution.
Then, we will proceed to define the Discrete Fourier Transform in summation form, (pointwise) and prove two of its fundamental theorems.
We use the Mathematical Components Libraries from INRIA and Microsoft Research. It is remarkable how close we can remain to the source in our theorem proving system.
Basic Circular Signal theory
Definition of Signals
Shifting of a signal.
$$ \shift_{d,n} x = x(n-d) $$Circular Convolution of two Signals
$$ (x \conv y)_n = \sum_{m=0}^{N-1} x(m) y(n-m) $$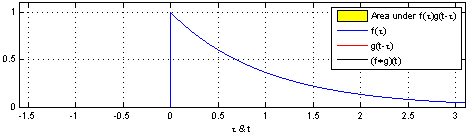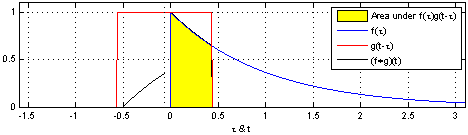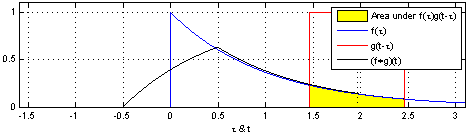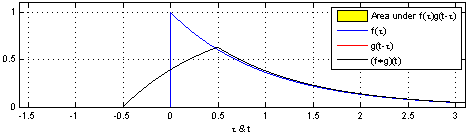
Credits: Wikipedia/Brian Amberg
Now we can do our first non-trivial proof using Coq! Let's see how the paper proof compares:
"In the first step we made the change of summation variable $l \equiv n-m$, and in the second step, we made use of the fact that any sum over all $ N$ terms is equivalent to a sum from 0 to $N-1$".
The DFT in sum form:
$$ \dft_k x = \sum_{m=0}^{N-1} x_m \omega^{km} $$The Shift Theorem:
$$ \dft_k[\shift_\Delta(x)] = \omega^{k\Delta} \dft_k x $$Proof: (from https://ccrma.stanford.edu/~jos/mdft/Shift_Theorem.html)
$$ \begin{eqnarray*} \dft_k[\shift_\Delta(x)] &\triangleq& \sum_{n=0}^{N-1} x(n-\Delta) \omega^{nk} \\ &=& \sum_{m=-\Delta}^{N-1-\Delta} x(m) \omega^{(m+\Delta) k} \qquad(m \equiv n-\Delta) \\ &=& \sum_{m=0}^{N-1}x(m) \omega^{mk} \omega^{k\Delta} \\ &=& \omega^{k \Delta} \sum_{m=0}^{N-1} x(m) \omega^{mk} \\ &\triangleq& \omega^{k\Delta} \dft_k x \end{eqnarray*} $$